Link Search Menu Expand Document
App 開發基礎

演算法和資料結構

11. 什麽是演算法?

1960 年代發明的結構化程式設計（Structured programming 是一種編程典範。它採用函式、程式碼區塊、for循環以及while循環等結構，來取代傳統的 goto語法。希望藉此來改善電腦程式的明晰性、品質以及開發時間，並且避免寫出面條式代碼。」程式從可以隨便跳來跳去的 goto 寫法，變成限製成三種流程控制：循序(prodecure)、分歧(if-else)、反復(while loop)。因此算法也是由這三大基礎結構所構成。

現今的程式語言幾乎都有這些特性，成為「常識」：流程控制(Flow control)和函數(function)

所謂的算法是一種有次序、明確定義和可行，最終會結束、有輸出的可執行步驟。雖然你可以用各種方式來描述一個算法，例如畫一個流程圖也可以是算法，但是對程序員來說，使用結構化形式來描述解決問題的詳細步驟，是最常見的方式。

例如，這是一個給陣列求最大值的算法，先假設第一個元素最大，然後依序走訪陣列每一個元素，檢查哪一個比較對就指派給 max 變數。最後跑完剩下來的 max 就是最大值。

def find_max(arr)
  max = arr[0]

  arr.each do |a|
    if a > max
      max = a
    end
  end

  return max
end

這個算法看起來非常簡單，它的基本思維就是暴力搜尋技術，這是非常基本的解決問題方式：把所有可能的解答都計算過一次，然後從裡面挑一個最棒的。

12. 如何評估演算法

一個算法好不好，要怎麽評估呢？電腦科學家特別關心當數據越來越多時，一個算法需要耗費多少時間。

我們使用一種叫做 Big-O 的符號來描述算法的複雜度，複雜度可以分成時間複雜度和空間複雜度，前者計算這個算法要花多少步驟，後者則是耗費多少記憶體空間。通常我們比較關心前者，以下介紹時間複雜度。

def constant(n)
  result = n * n
  result = result + 1

  return result
end

這個 constant 方法，不管 n 是多少，執行的步驟都是固定的，執行時間都一樣，科學者於是稱之這個時間複雜度是 O(1)是常數的。

def linear(n)
  sum = 0
  1.upto(n) do |i|
    sum = sum + i
  end

  return sum
end

這個 linear 方法，當 n 越大的時候，裡面的循環就得跑越多次，這時間複雜度為 O(n) 是線性的：當 n 成長十倍時，需要的執行時間也是十倍。

def quadratic(n)
  sum = 0
  1.upto(n) do |i|
    1.upto(n) do |j|
      sum = sum + i + j
    end
  end

  return sum
end

這個 quadratic 方法，當 n 越大的時候，裡面的循環就得平方多次，這時間複雜度為 O(n^2) 是平方的：當 n 成長十倍時，需要的執行時間是一百倍。

def logarithmic(n)
  result = 0
  while n > 1
    n = n.to_f / 2
    result += 1
  end

  return result
end

這個 logarithmic 方法的 Big-O 是 O(log n)，當 n 成長從 100 變成 100000 時，需要的執行時間是 2.5 倍而已。

以下是不同 Big-O 的成長圖表

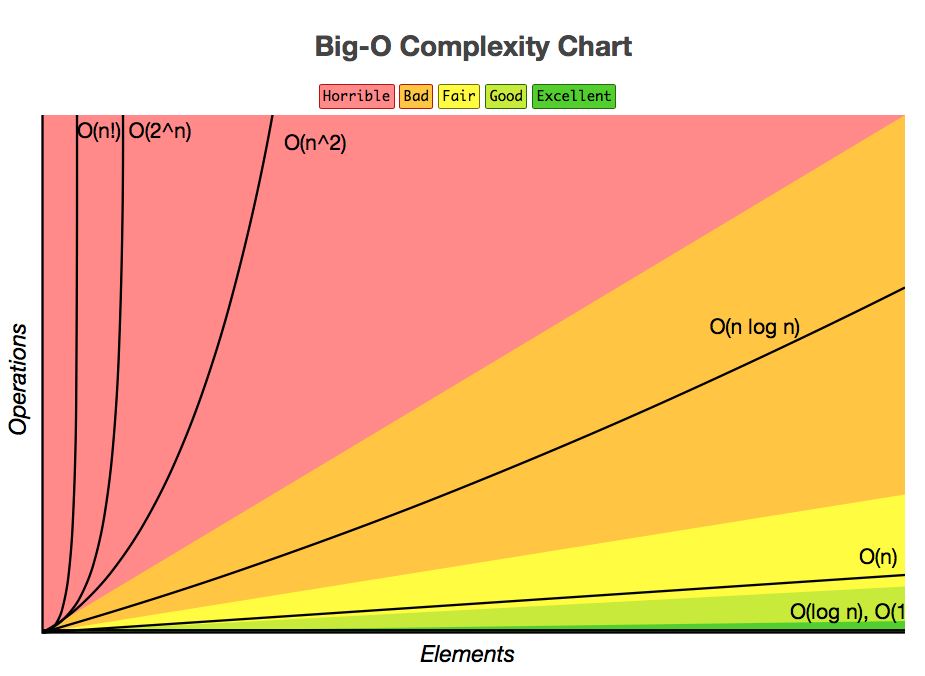
image

在電腦本科生的算法課程中，會非常詳細的去分析和評估算法的複雜度。例如經典的案例就是陣列的排序算法。我們在上一堂課中，曾經要求大家練習選擇排序法。如果你有練習的話，這個算法內的循環內還有一個循環，這是一個 O(n^2) 的算法。世界上有各式各樣的排序算法，在算法課中就會去示範分析每一種算法的優缺點，要多少複雜度。

不同排序算法示範：

其中證明了最好的就是 O(nlogn)，像 Ruby 的 Array#sort 方法就是用快速排序法做的。

還有，在編程基礎練習中，有一題是在陣列中找到最大(或最小)的數字，例如 arr = [5,1,9,4]，以下兩種算法都可以得到答案：

第一種：

def find_max(arr)
  max = arr[0]

  arr.each do |a|
    if a > max
      max = a
    end
  end

  return max
end

第二種：

def find_max(arr)
  arr.sort.last
end

第二種看起來比較簡單，但是現在你可以判斷第一種方法是 O(n)，第二種確是 O(nlogn) 了，前者比較好。

當然，Ruby 可以直接調用 arr.max 方法，就得到第一種方法的結果

13. 什麽是資料結構?

資料結構定義資料之間的相互關系，是設計算法的載體，數據輸入輸出和設計算法步驟時，都會對應於使用的資料結構。而不同的資料結構有不同的特性。在電腦本科生的課程中，有門資料結構的課，就是在分析各種不同的資料結構，做不同操作時的優點點和複雜度：Common Data Structure Operations

對 Ruby 程序員來說，最常用的就是 Array 和 Hash，我們在組合數據類型介紹過 Array 和 Hash 內部原理，現在我們來分析一下常用的操作，對 Array 和 Hash 的算法複雜度。

插入和刪除到容器裡面

要在陣列中插入一個值，如果剛好在最後(例如 Arrar#push 方法)，是 O(1) 如果在陣列中間插入一個值，因為陣列是記憶體中「連續」的空間，中間新插入，會需要搬動後面所有元素的位置往後移動一格，這是 O(n) 的算法，n 越大需要移動的元素越多。

對雜湊 Hash 來說，插入是平均複雜度是 O(1)。

檢查一個值都沒有在容器裡面

Array 是 O(n)，需要走訪整個陣列依序檢查

Hash 是 O(1)，只要將 key 經過雜湊算法，就可以直接檢查那個位置有沒有數據。

讓我們動手實驗看看，Ruby 內建有 benchmark 工具，可以讓我們量測一個方法的執行時間：

require 'benchmark'

a1 = Array.new(1000000){ rand(100) } # 造一個一百萬個元素的陣列，內容是亂數
a2 = a1 * 10   # 陣列放大十倍

h1 = {}
a1.each { |x| h1[x] = :y } # 把陣列轉成雜湊

h2 = {}
a2.each { |x| h2[x] = :y }


Benchmark.bm do |x|
  x.report {
    a1.include?(999)
  }
  x.report {
    a2.include?(999)
  }
  x.report {
    h1[999] == :y
  }
  x.report {
    h2[999] == :y
  }
end

這個實驗檢查容器裡面有沒有 999 這個值，這是結果：

       user     system      total        real
   0.000000   0.000000   0.000000 (  0.005854) # 陣列一
   0.060000   0.010000   0.070000 (  0.064084) # 十倍大的陣列二：時間約成長 10 倍
   0.000000   0.000000   0.000000 (  0.000005) # 雜湊一:
   0.000000   0.000000   0.000000 (  0.000005) # 十倍大的雜湊二: 時間一樣

你會發現需要的時間，陣列需要的時間約增加了十倍，但是雜湊卻一樣。

資料庫打索引的原理也是一樣的，沒有打索引就是 O(n)，有打索引是 O(logn)。當資料庫成長到上百萬筆資料時，有沒有索引的時間差距是很大的。資料庫內部用的索引資料結構是 B-tree

14. 演算法的極限

這一節我們探討一個有趣的問題，電腦這麽厲害，有沒有不能計算的問題？

有的，例如停機問題：你沒辦法寫一個軟體，去判斷另一個軟體會不會當機。所以說 Apple 審核不可能審核到你的 App 會不會當機。

另外，有些問題雖然可以計算，但是算法耗費太多資源或時間，這種問題的最佳解 Big-O 是 O(2^N)，而非多項式時間內。因此要求最佳解是不切實際的，只能用最佳化逼近解。

我們可以看看 O(2^N) 有多恐怖，當 N = 100 時，就比大霹靂以來的微秒數還要多。沒有電腦可以在我們有生之年可以計算完畢。最近的熱門話題 AlphaGo 下圍棋之所以這麽了不起，就是因為就算現代電腦這麽先進了，也不可能窮舉所有的可能來下圍棋。

已知最佳解就是 O(2^N) 的算法問題，就叫做 NP 類型的算法問題，例如河內塔步驟：假設有 N 個的環，那麽最佳解的移動步驟是 2^N - 1，原始版本和尚要移動 64 個環根本就不可能。其他像是西洋棋必勝策略也是 NP 類型問題。

已知有指數時間解，但是不確定有沒有更好的多項式時間解，這就作 NP-Complete 類型的問題。例如 旅行推銷員問題是 O(n!) n階層時間。

P = NP 是 在理論信息學中計算複雜度理論領域里至今沒有解決的問題。

15. 推薦書籍

這門教程的知識點非常多，包括了電腦大學本科 1. 資料結構 2. 算法 3. 作業系統 4. 編譯器 5. 程式語言，大一到大三共五門必修課程的主要概念。我推薦以下書籍可以繼續進修：

放心，這些都不是大部頭的教科書

16. 關於演算法和找工作面試

有些公司很愛考算法題目，特別是大型公司，例如 Google、Microsof、Facebook、BAT 等大企業。因為他們偏好學歷好電腦本科系剛畢業，聰明、底子好的學生，不看重作品集，招聘後再內訓。

如果你對這類型公司有偏好，你需要熟悉各種資料結構的操作算法，例如 Stack、Queue、Linked List、Tree、Graph 等等。

基本的解題策略是：先很快的用暴力解(Brute-force)，先別擔心算法效率。然後再最佳化，找出哪些步驟是多餘重復的計算。通常考官都會逐步提示你完成最佳化。

你需要花時間練習熟悉題型，例如：

就算是大神，碰到這種公司不先刷題也是被拒的。

在大學的演算法課程中，也會教授一些常見的算法模式，例如：

練習作業

給定一個陣列，請寫出一個方法，找出裡面重復的數字。例如

  • 輸入 [1,1,2] 回傳 [1]
  • 輸入 [1,1,2,2] 回傳 [1,2]
  • 輸入 [1,2,3] 回傳 []

請分析以下兩種解法的複雜度，並貼上 benchmark 對比的結果，哪一個算法比較好：

練習作業

Ruby 的 Array#find_index 方法可以從陣列中尋找一個值，回傳它的索引，這個算法是 O(n)。

arr = [5,1,9,6]
arr.find_index(9) # 回傳 2

Ruby 還有一個 Array#bsearch，實作了 二分搜索算法 binary search。如果你已知陣列是排序過的，這個算法會是 O(log n)。

請自行實作一個 Binary Search 算法，並且 benchmark 比較當 arr 元素有10個、10000個、1000000 個時，平均(或最糟)需要多少運算時間。

把答案和 Benchmark 結果貼在 https://gist.github.com 然後作業繳交 gist 網址：

def binary_search(arr, element)
 # .... 你的實作放這裡
end

arr = [0, 5, 13, 13, 30, 42, 52, 70, 85, 96, 103, 111, 116, 127, 130, 143, 150, 150, 161, 175, 207, 210, 218, 246, 257, 257, 263, 280, 304, 310, 326, 327, 332, 346, 360, 371, 374, 378, 406, 407, 407, 408, 428, 431, 437, 442, 445, 479, 489, 491, 505, 517, 520, 536, 548, 598, 602, 605, 618, 642, 649, 654, 659, 662, 677, 678, 682, 689, 695, 696, 697, 701, 711, 717, 727, 737, 745, 749, 754, 757, 770, 786, 802, 805, 814, 832, 840, 850, 853, 854, 888, 894, 904, 913, 913, 945, 962, 964, 972, 998]

binary_search(arr, 371) # 應該回傳 35

當然，如果陣列沒有排序過，你要先排序才能調用二分搜尋算法，就是先排序就會是 O(n logn) 了。

補充閱讀

Copyright © 2010-2022 Wen-Tien Chang All Rights Reserved.